¿Qué tienen en común Bill Gates, Los Simpson y la E. Coli? Una torre de tortitas

A cualquier matemático que se precie le gustan los retos. Donde uno sólo ve letras y números, un aficionado a las 'mates' encuentra un desafío que hay que superar. Y si ese desafío resulta que no lo ha conseguido resolver ningún matemático anterior, el fanático de las ecuaciones estalla en euforia cuando logra encontrar el resultado.
No es necesario rebuscar en libros y manuales para encontrar un reto de este tipo. A veces, los problemas más emocionantes proceden de situaciones tan comunes como doblar y colocar toallas en el armario del baño.
En una circunstancia como ésta se hallaba el matemático estadounidense Jacob E. Goodman cuandio descubrió el problema del 'pancake'. El reto que atrajo a David X. Cohen, guionista de Los Simpson, y al mismísimo Bill Gates.

El problema de las tortitas
La faceta científica del fundador de Microsoft apenas se conoce. Solo ha publicado una investigación en toda su carrera, en 1979 y en compañía del informático griego Christos Papadimitriou. Un estudio en el que trató de esclarecer el problema que Goodman había teorizado cuatro años antes.
Tal y como cuenta el matemático Simon Singh en su libro 'Los Simpson y las matemáticas', el problema del 'pancake' nació cuando Goodman se encontraba doblando y colocando toallas en el armario del baño de su casa. Parecía una tarea sencilla: bastaba con poner las grandes primero y las pequeñas en último lugar.
Sin embargo, la cosa se complicó cuando necesitó colocar más telas en el estante. Como no cabían todas, tuvo que dar la girar varias de las toallas de arriba y volver a ordenarlas. Y entre vuelta y vuelta, le llegó la inspiración: “¿cuántas veces tendría que girar grupos de toallas, en el peor de los casos, para conseguir disponerlas de mayor a menor?”
Pensó que sería interesante publicar el problema en la revista American Mathematical Monthly, pero las toallas resultaban de lo más inverosímil, así que decidió sustituir las telas por tortitas ('pancakes', en inglés). Asimismo, en aquella época, Goodman se estaba haciendo un nombre en el mundo de las matemáticas, y vincular sus apellidos a un acertijo matemático no le otorgaba mucha seriedad. De ahí que el problema del 'pancake' tuviera la firma de Harry Dweigther, un juego de palabras que significa 'Harry, el camarero'.
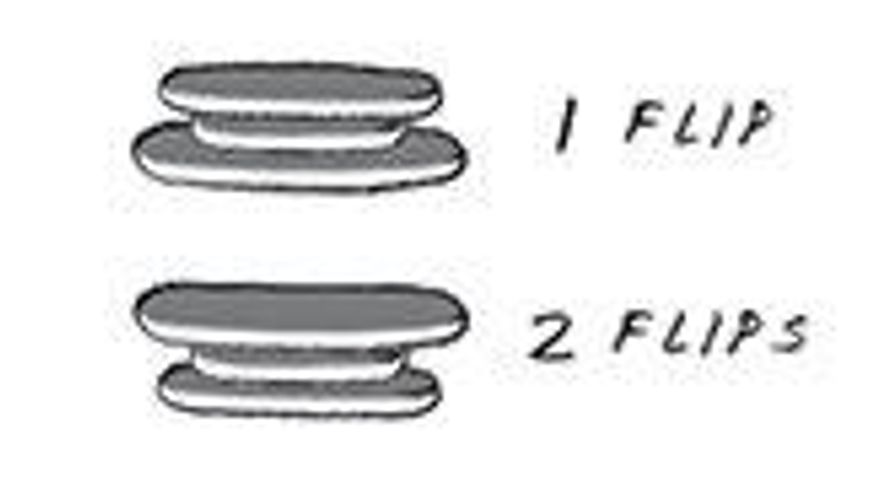
Dicho camarero planteó el problema de la siguiente forma: “el chef en nuestro establecimiento es descuidado, y cuando prepara una torre de tortitas las hace de diferentes tamaños. Cuando se las servimos al cliente, de camino a la mesa, las arreglo (las más pequeñas en la cima y las más grandes en la base), cogiendo varias de la cima y girándolas, y repitiendo la operación tantas veces como sea necesario. Si hay n tortitas, ¿cuál es el número máximo de giros (en función de n) que tengo que dar para volver a colocar las tortitas?”
Lo interesante del asunto es que aún, más de treinta años después, no se ha dado con la respuesta a dicha pregunta. Se ha intentado, eso sí, acotar el resultado y ver más o menos por donde podría andar la solución. La investigación de Gates y Papadimitriou dio con la ecuación que calcula el número máximo de giros - no exacto, sino aproximado - que podrían ser necesarios para reordenar cualquier número de tortitas apiladas. Introdujo, además, una nueva versión de la adivinanza: el problema de los 'pancakes' quemados.

Si están quemadas, mucho mejor
Gates y Papadimitriou imaginaron que al chef se le habían quemado las tortitas por uno de los lados, de tal forma que, a la hora de servirlas, habría que colocarlas con la parte tostada debajo y el lado bonito al descubierto. Algo que complicaría la tarea.
A pesar de que tampoco se conoce la respuesta a la pregunta “¿cuál es el número máximo de giros (en función de n) que tengo que realizar para volver a ordenar las tortitas y hacerlo, además, por la parte sin quemar?”, en 1995, David X. Cohen, físico, informático y también guionista de Los Simpson, junto con quince autores más, averiguó la ecuación que calculaba el número máximo y mínimo de giros que tendrían que realizarse. En su libro, Singh pone como ejemplo las veces que habría que reorganizar 1.000 tortitas en el peor de los escenarios posibles, que serían entre 1.500 y 1998.
Puede resultar extraño, pero el acertijo de Goodman y la versión de Gates y Papadimitriou tienen aplicaciones en la vida real. En concreto, en el campo de la informática y la biología. El hecho de colocar y recolocar tortitas se asemeja bastante al problema al que se enfrenta un programador a la hora de organizar y reorganizar estructuras de datos, y a los biólogos les resulta fascinante aquello de que diferentes organismos compartan los mismos genes ordenados de forma distinta.
El último hallazgo científico que tenemos que agradecer al problema de las tortitas quemadas se produjo en 2008, cuando un grupo de investigadores de la Universidad de Missouri Oeste y el Davidson College modificó la genética de las bacterias E. Coli. Los fragmentos de ADN insertados representaban los 'pancakes' quemados de Gates y la forma en que las bacterias los ordenaron demostró que las estructuras generadas por la E. Coli se pueden almacenar, como un ordenador guarda los datos. No veas si da juego una torre de tortitas...
---------------------------------------
Las imágenes de este artículo son propiedad, por orden de aparición, de Hedvigs, Wikimedia Commons, Los Simpson y las matemáticas (libro) y UCFFool




